In order to perform Cholesky Decomposition of a matrix, the matrix has to be a positive definite matrix. I have listed down a few simple methods to test the positive definiteness of a matrix.
Methods to test Positive Definiteness:
Remember that the term positive definiteness is valid only for symmetric matrices.
Test method 1: Existence of all Positive Pivots
For a matrix to be positive definite, all the pivots of the matrix should be positive. Hmm.. What is a pivot ?
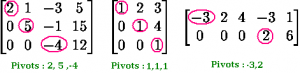
Pivots:
Pivots are the first non-zero element in each row of a matrix that is in Row-Echelon form. Row-Echelon form of a matrix is the final resultant matrix of Gaussian Elimination technique.
In the following matrices, pivots are encircled.
A positive definite matrix will have all positive pivots. Only the second matrix shown above is a positive definite matrix. Also, it is the only symmetric matrix.
Test method 2: Determinants of all upper-left sub-matrices are positive:
Determinant of all $latex k \times k $ upper-left sub-matrices must be positive.
Break the matrix in to several sub matrices, by progressively taking $latex k \times k $ upper-left elements. If the determinants of all the sub-matrices are positive, then the original matrix is positive definite.
Is the following matrix Positive Definite?

Find the determinants of all possible $latex k \times k $ upper sub-matrices.

Test method 3: All Positive Eigen Values
If all the Eigen values of the symmetric matrix are positive, then it is a positive definite matrix.
Is if following matrix Positive definite ?

Since, not all the Eigen Values are positive, the above matrix is NOT a positive definite matrix.
There exist several methods to determine positive definiteness of a matrix. The method listed here are simple and can be done manually for smaller matrices.
Rate this article: [ratings]
External resource:
1) Online tool to generate Eigen Values and Eigen Vectors↗
Books by the author
[table id=23/]
See also:
[table id=7 /]