Generate two correlated random sequences

by

[ratings]

This article discusses the method of generating two correlated random sequences using Matlab. If you are looking for the method on generating multiple sequences of correlated random numbers, I urge you to go here.

Generating two vectors of correlated random numbers, given the correlation coefficient $latex \rho$, is implemented in two steps. The first step is to generate two uncorrelated random sequences from an underlying distribution. Normally distributed random sequences are considered here.

[table id = 36/]

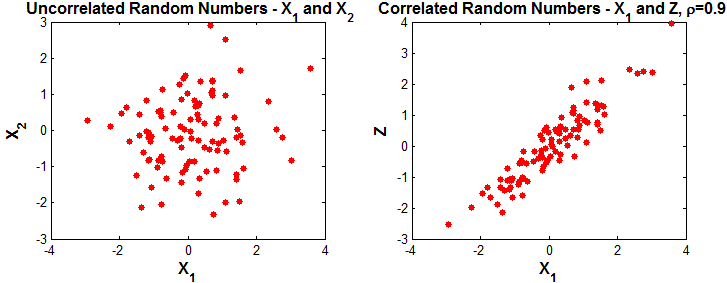
Step 1: Generate two uncorrelated Gaussian distributed random sequences $latex X_1, X_2$

x1=randn(1,100); %Normal random numbers sequence 1
x2=randn(1,100); %Normal random numbers sequence 2
subplot(1,2,1); plot(x1,x2,'r*');
title('Uncorrelated RVs X_1 and X_2');
xlabel('X_1'); ylabel('X_2');

Step 2: Generate correlated random sequence z

In the second step, the required correlated sequence is generated as

$latex Z=\rho X_1 + \sqrt{1-\rho^2} X_2 &s=2$

rho=0.9;
z=rho*x1+sqrt(1-rhoˆ2)*x2;%transformation
subplot(1,2,2); plot(x1,z,'r*');
title(['Correlated RVs X_1 and Z , \rho=',num2str(rho)]);
xlabel('X_1'); ylabel('Z');

The resulting sequence Z will have $latex \rho$ correlation with respect to $latex X_1$

Results plotted below.

Scatter plot of Two Correlated Random sequences that were generated
Figure : Scatter plots – Correlated random variables $latex Z$ and $latex X_1$ on right

Continue reading this article on the method to generate multiple vectors of correlated random numbers.

Rate this article: [ratings]

Further reading

[1] Richard Taylor, “Interpretation of correlation coefficient: A basic review”, Journal of diagnostic medical sonography, Jan/Feb 1990.↗

Topics in this chapter

[table id=33 /]

Books by the author

[table id=23 /]

Leave a Comment