Solving ARMA model – minimization of squared error

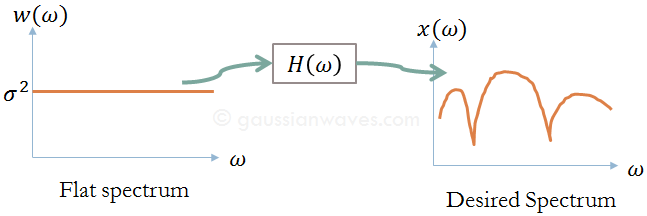
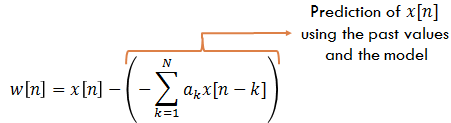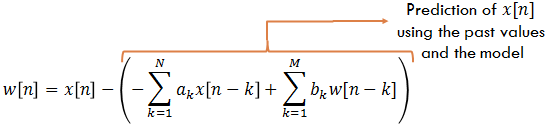Key focus: Can a unique solution exists when solving ARMA (Auto Regressive Moving Average) model ? Apply minimization of squared error to find out.

As discussed in the previous post, the ARMA model is a generalized model that is a mix of both AR and MA model. Given a signal x[n], AR model is easiest to find when compared to finding a suitable ARMA process model. Let’s see why this is so.

AR model error and minimization

In the AR model, the present output sample x[n] and the past N-1 output samples determine the source input w[n]. The difference equation that characterizes this model is given by

$latex x[n] + a_1 x[n-1] + a_2 x[n-2] + \cdots + a_N x[n-N] = w[n] &s=1$

The model can be viewed from another perspective, where the input noise w[n] is viewed as an error – the difference between present output sample x[n] and the predicted sample of x[n] from the previous N-1 output samples. Let’s term this “AR model error“. Rearranging the difference equation,

$latex \displaystyle{ w[n]= x[n]-\left(-\sum^{N}_{k=1}a_k x[n-k] \right)} &s=1$

The summation term inside the brackets are viewed as output sample predicted from past N-1 output samples and their difference being the error w[n].

Least squared estimate of the co-efficients – a_k are found by evaluating the first derivative of the squared error with respect to a_k and equating it to zero – finding the minima.From the equation above, w²[n] is the squared error that we wish to minimize. Here, w²[n] is a quadratic equation of unknown model parameters a_k. Quadratic functions have unique minima, therefore it is easier to find the Least Squared Estimates of a_k by minimizing w²[n].

ARMA model error and minimization

The difference equation that characterizes this model is given by

$latex \begin{aligned} x[n] + a_1 x[n-1] + \cdots + a_N x[n-N] = & b_0 w[n] + b_1 w[n-1] + \\ & \cdots + b_M w[n-M] \end{aligned}&s=1$

Re-arranging, the ARMA model error w[n] is given by

$latex \displaystyle{ w[n]= x[n]-\left(-\sum^{N}_{k=1}a_k x[n-k] + \sum^{M}_{k=1}b_k w[n-k] \right)} &s=1$

Now, the predictor (terms inside the brackets) considers weighted combinations of past values of both input and output samples.

The squared error, w²[n] is NOT a quadratic function and we have two sets of unknowns – a_k and b_k. Therefore, no unique solution may be available to minimize this squared error-since multiple minima pose a difficult numerical optimization problem.

Rate this article: [ratings]

Related topics:

[table id=7 /]

For further reading

[1] Thiesson et al, “ARMA time series modeling with graphical models”, Proceedings of the Twentieth Conference on Uncertainty in Artificial Intelligence, July 2004↗

Books by the author

[table id =23/]