[ratings]
If squares of k independent standard normal random variables are added, it gives rise to central Chi-squared distribution with ‘k’ degrees of freedom. Instead, if squares of k independent normal random variables with non-zero means are added, it gives rise to non-central Chi-squared distribution. Non-central Chi-square distribution is related to Ricean distribution, whereas the central Chi-squared distribution is related to Rayleigh distribution.
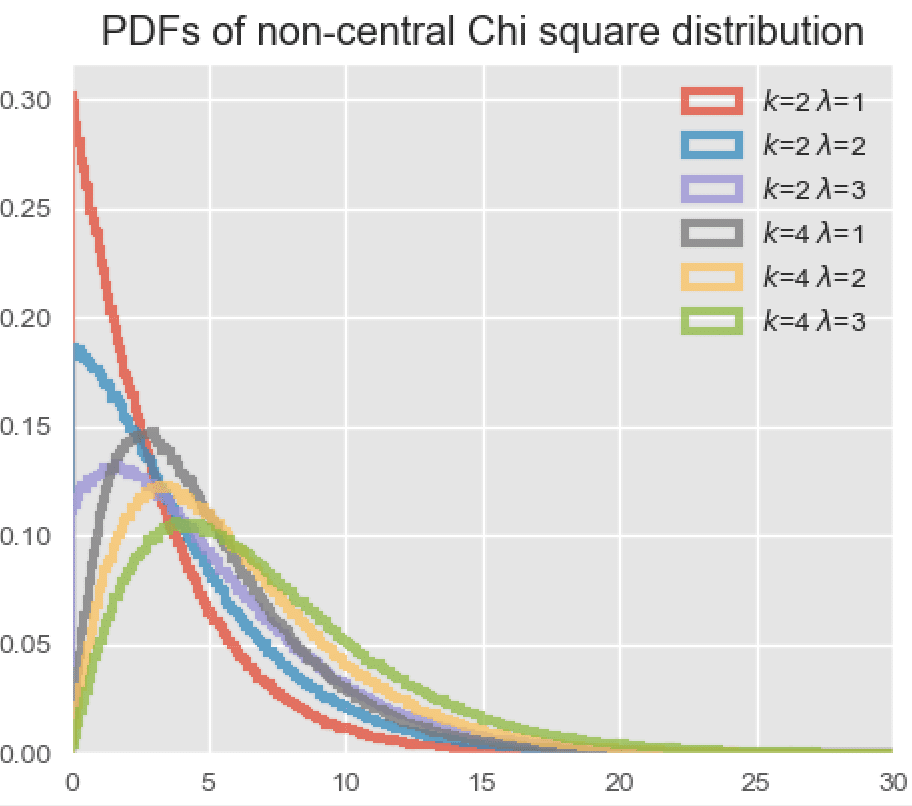
The non-central Chi-squared distribution is a generalization of Chi-square distribution. A non-central Chi squared distribution is defined by two parameters: 1) degrees of freedom ($latex k$) and 2) non-centrality parameter $latex \lambda$.
As we know from previous article, the degrees of freedom specify the number of independent random variables we want to square and sum-up to make the Chi-squared distribution. Non-centrality parameter is the sum of squares of means of the each independent underlying normal random variable.
The non-centrality parameter is given by
$latex \lambda = \displaystyle{\sum_{i=1}^k \mu_i^2} \quad\quad\quad (1) &s=2$
The PDF $latex f_{\chi_k^2} (x, \lambda)$ of the non-central Chi-squared distribution having $latex k$ degrees of freedom and non-centrality parameter $latex \lambda $ is given by
$latex f_{\chi_k^2} (x, \lambda) = \displaystyle{\sum_{n=0}^{\infty} \frac{e ^{- \lambda/2 } \left(\lambda/2 \right )^n}{n!} f_{Y_{k+2n}} (x)} \quad\quad\quad (2) &s=2$
Here, the random variable $latex Y_{k+2n}$ is central Chi-squared distributed with $latex k+2n$ degrees of freedom. The factor $latex \frac{e ^{- \lambda/2 } \left(\lambda/2 \right )^n}{n!}$ gives the probabilities of Poisson distribution. Thus, the PDF of the non-central Chi-squared distribution can be termed as the weighted sum of Chi-squared probabilities where the weights being equal to the probabilities of Poisson distribution.
Method of Generating non-central Chi-squared random variable:
The procedure for generating the samples from a non-central Chi-squared random variable is as follows.
● For a given degree of freedom $latex k$, let the $latex k$ normal random variables be $latex X_1,X_2,\cdots,X_k$ with variances $latex \sigma_1^2,\sigma_2^2,\cdots,\sigma_k^2$ and mean $latex \mu_1,\mu_2,\cdots,\mu_k$ respectively.
● The goal is to add squares of these $latex k$ independent normal random variables with variances set to one and means satisfying the condition set by equation (1).
● Set $latex \mu_1= \sqrt{\lambda} $ and $latex \mu_2,\mu_3,\cdots,\mu_k=0$
● Generate $latex k-1$ standard normal random variables $latex \sim \mathit{N}(\mu=0,\sigma^2=1) $ and one normal random variable with $latex \mu_1= \sqrt{\lambda}$ and $latex \sigma_1^2=1$
● Squaring and summing-up all the $latex k$ random variables gives the non-central Chi-squared random variable.
● The PDF of the generated samples can be plotted using the histogram method described here.
Matlab Code:
Check this book for full Matlab code.
Wireless Communication Systems using Matlab – by Mathuranathan Viswanathan
Python Code:
Python numpy package has a nocentral_chisquare() generator, which can be used in a straightforward manner to obtain the non-central Chi square distributed sequences.
#---------Non-central Chi square distribution gaussianwaves.com-----
import numpy as np
import matplotlib.pyplot as plt
#%matplotlib inline
plt.style.use('ggplot')
ks=np.asarray([2,4]) #degrees of freedoms to simulate
ldas = np.asarray([1,2,3]) #non-centrality parameters to simulate
nSamp=1000000 #number of samples to generate
fig, ax = plt.subplots(ncols=1, nrows=1, constrained_layout=True)
for i,k in enumerate(ks):
for j,lda in enumerate(ldas):
#Generate non-central Chi-squared distributed random numbers
X = np.random.noncentral_chisquare(df=k, nonc = lda, size = nSamp)
ax.hist(X,bins=500,density=True,label=r'$k$={} $\lambda$={}'.format(k,lda),\
histtype='step',alpha=0.75, linewidth=3)
ax.set_xlim(left=0,right=30);ax.legend()
ax.set_title('PDFs of non-central Chi square distribution');
plt.show()Rate this article: [ratings]
For further reading
Similar topics
[table id = 33/]
Books by the author
[table id=23/]