In wireless environments, transmitted signal may be subjected to multiple scatterings before arriving at the receiver. This gives rise to random fluctuations in the received signal and this phenomenon is called fading. The scattered version of the signal is designated as non line of sight (NLOS) component. If the number of NLOS components are sufficiently large, the fading process is approximated as the sum of large number of complex Gaussian process whose probability-density-function follows Rayleigh distribution.
Rayleigh distribution is well suited for the absence of a dominant line of sight (LOS) path between the transmitter and the receiver. If a line of sight path do exist, the envelope distribution is no longer Rayleigh, but Rician (or Ricean). If there exists a dominant LOS component, the fading process can be represented as the sum of complex exponential and a narrowband complex Gaussian process g(t). If the LOS component arrive at the receiver at an angle of arrival (AoA) θ, phase ɸ and with the maximum Doppler frequency fD, the fading process in baseband can be represented as (refer [1])
where, K represents the Rician K factor given as the ratio of power of the LOS component A2 to the power of the scattered components (S2) marked in the equation above.
The received signal power Ω is the sum of power in LOS component and the power in scattered components, given as Ω=A2+S2. The above mentioned fading process is called Rician fading process. The best and worst-case Rician fading channels are associated with K=∞ and K=0 respectively. A Ricean fading channel with K=∞ is a Gaussian channel with a strong LOS path. Ricean channel with K=0 represents a Rayleigh channel with no LOS path.
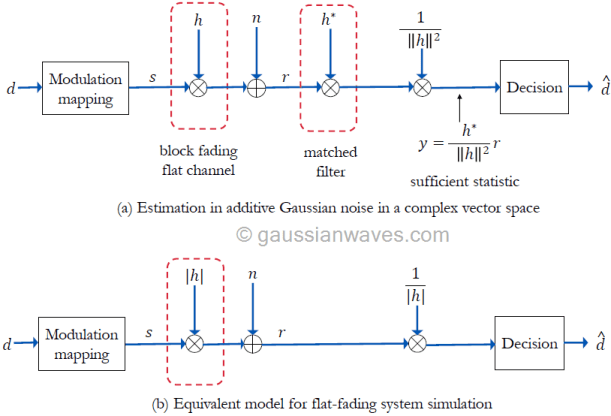
The statistical model for generating flat-fading Rician samples is discussed in detail in chapter 11 section 11.3.1 in the book Wireless communication systems in Matlab (see the related article here). With respect to the simulation model shown in Figure 1(b), given a K factor, the samples for the Rician flat-fading samples are drawn from the following random variable
where X,Y ~ N(μ,σ2) are Gaussian random variables with non-zero mean μ and standard deviation σ as given in references [2] and [3].
Simulation and performance results
In chapter 5 of the book Wireless communication systems in Matlab, the code implementation for complex baseband models for various digital modulators and demodulator are given. The computation and generation of AWGN noise is also given in the book. Using these models, we can create a unified simulation for code for simulating the performance of various modulation techniques over Rician flat-fading channel the simulation model shown in Figure 1(b).
An unified approach is employed to simulate the performance of any of the given modulation technique – MPSK, MQAM or MPAM. The simulation code (given in the book) will automatically choose the selected modulation type, performs Monte Carlo simulation, computes symbol error rates and plots them against the theoretical symbol error rate curves. The simulated performance results obtained for various modulations are shown in the Figure 2.
Rate this article: Note: There is a rating embedded within this post, please visit this post to rate it.
References
[1] C. Tepedelenlioglu, A. Abdi, and G. B. Giannakis, The Ricean K factor: Estimation and performance analysis, IEEE Trans. Wireless Communication ,vol. 2, no. 4, pp. 799–810, Jul. 2003.↗
[2] R. F. Lopes, I. Glover, M. P. Sousa, W. T. A. Lopes, and M. S. de Alencar, A simulation framework for spectrum sensing, 13th International Symposium on Wireless Personal Multimedia Communications (WPMC 2010), Out. 2010.
[3] M. C. Jeruchim, P. Balaban, and K. S. Shanmugan, Simulation of Communication Systems, Methodology, Modeling, and Techniques, second edition Kluwer Academic Publishers, 2000.↗
Books by the author
Wireless Communication Systems in Matlab Second Edition(PDF) Note: There is a rating embedded within this post, please visit this post to rate it. | Digital Modulations using Python (PDF ebook) Note: There is a rating embedded within this post, please visit this post to rate it. | Digital Modulations using Matlab (PDF ebook) Note: There is a rating embedded within this post, please visit this post to rate it. |
| Hand-picked Best books on Communication Engineering Best books on Signal Processing |
||