Signal Processing for Communication Systems
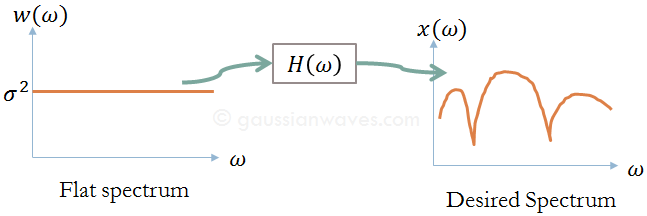
The agenda for the subsequent series of articles is to introduce the idea of autocorrelation, AutoCorrelation Function (ACF), Partial AutoCorrelation Function (PACF) , using ACF and PACF in system identification. Introduction Given time series data (stock market data, sunspot numbers over a period of years, signal samples received over a communication channel etc.,), successive values … Read more
If a time series data is assumed to be following an Auto-Regressive (\(AR(N)\)) model of given form, the natural tendency is to estimate the model parameters \(a_1,a_2, \cdots, a_N\). Least squares method can be applied here to estimate the model parameters but the computations become cumbersome as the order \(N\) increases. Fortunately, the AR model … Read more
Key focus: “Why can’t I just use a matrix to solve ARMA?” The answer is right there in the shape of the surface—you can’t solve a “warped” landscape with a linear equation. Introduction In signal modeling, our goal is to find a set of coefficients (ak and bk) that best describe an observed signal. We … Read more
Key focus: AR, MA & ARMA models express the nature of transfer function of LTI system. Understand the basic idea behind those models & know their frequency responses. How do you describe a complex, random signal—like the sound of a human voice or the fluctuating power of a fading channel—using only a few numbers? The … Read more