Signal Processing for Communication Systems
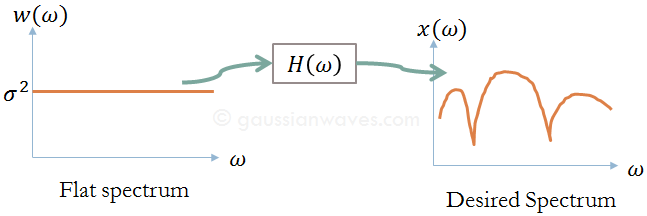
Key focus: Learn how to generate color noise using auto regressive (AR) model. Apply Yule Walker equations for generating power law noises: pink noise, Brownian noise. Auto-Regressive (AR) model An uncorrelated Gaussian random sequence \(x[n]\) can be transformed into a correlated Gaussian random sequence \(y[n]\) using an AR time-series model. If a time series random … Read more
The aim of this article is to demonstrate the application of spectral factorization method in generating colored noise having Jakes power spectral density. Before continuing, I urge the reader to go through this post: Introduction to generating correlated Gaussian sequences. In spectral factorization method, a filter is designed using the desired frequency domain characteristics (like … Read more
Key focus: Colored noise sequence (a.k.a correlated Gaussian sequence), is a non-white random sequence, with non-constant power spectral density across frequencies. Introduction Speaking of Gaussian random sequences such as Gaussian noise, we generally think that the power spectral density (PSD) of such Gaussian sequences is flat.We should understand that the PSD of a Gausssian sequence … Read more
The agenda for the subsequent series of articles is to introduce the idea of autocorrelation, AutoCorrelation Function (ACF), Partial AutoCorrelation Function (PACF) , using ACF and PACF in system identification. Introduction Given time series data (stock market data, sunspot numbers over a period of years, signal samples received over a communication channel etc.,), successive values … Read more
If a time series data is assumed to be following an Auto-Regressive (\(AR(N)\)) model of given form, the natural tendency is to estimate the model parameters \(a_1,a_2, \cdots, a_N\). Least squares method can be applied here to estimate the model parameters but the computations become cumbersome as the order \(N\) increases. Fortunately, the AR model … Read more
Key focus: “Why can’t I just use a matrix to solve ARMA?” The answer is right there in the shape of the surface—you can’t solve a “warped” landscape with a linear equation. Introduction In signal modeling, our goal is to find a set of coefficients (ak and bk) that best describe an observed signal. We … Read more
Key focus: AR, MA & ARMA models express the nature of transfer function of LTI system. Understand the basic idea behind those models & know their frequency responses. How do you describe a complex, random signal—like the sound of a human voice or the fluctuating power of a fading channel—using only a few numbers? The … Read more