The Shannon power efficiency limit is the limit of a band-limited system irrespective of modulation or coding scheme. It informs us the minimum required energy per bit required at the transmitter for reliable communication. It is also called unconstrained Shannon power efficiency Limit. If we select a particular modulation scheme or an encoding scheme, we calculate the constrained Shannon limit for that scheme.
Before proceeding, I urge you to go through the fundamentals of Shannon Capacity theorem in this article.
[table id=36 /]
Channel capacity and power efficiency
One of the objective of a communication system design is to reliably send information at the lowest possible power level. The system should be able to provide acceptable bit-error-rate (BER) performance at the lowest possible power level. Often, this performance is charted in terms of BER Vs. $latex E_b/N_0$. The quantity $latex E_b/N_0$ is called power efficiency, denoted as $latex \eta_P$. Power efficiency is defined as the ratio of signal energy per bit ($latex E_b$) to noise power spectral density per bit ($latex N_0$ – required at the receiver input to achieve certain BER.
$latex \eta_P = \frac{E_b}{N_0} \quad \quad (1) &s=2$
From equations (1) and (2) shown in this post, the condition for reliable transmission through a channel is given by
$latex \eta_B = \frac{R}{B} < \frac{C}{B} = log_2 \left( 1 + \frac{E_b R}{N_0 B} \right) \quad \quad (2) &s=2$
Re-writing in terms of spectral efficiency $latex \eta_B$, the Shannon limit on power efficiency $latex \eta_P$ for reliable communication is given by
$latex \frac{E_b}{N_0} > \frac{2^{\eta_B} – 1}{\eta_B}\quad \quad (3) &s=2$
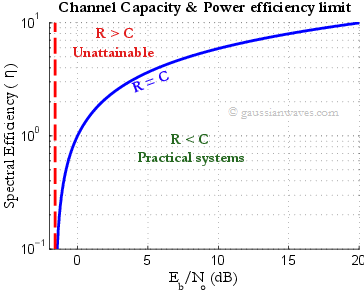
With this equation, we can calculate the minimum $latex E_b/N_0$ required to achieve a certain spectral efficiency. As an example, lets simulate and plot the relationship between $latex E_b/N_0$ and spectral efficiency $latex \eta_B$, as given in equation (3).
k =0.1:0.001:15; EbN0=(2.ˆk-1)./k;
semilogy(10*log10(EbN0),k);
xlabel('E_b/N_o (dB)');ylabel('Spectral Efficiency (\eta)');
title('Channel Capacity & Power efficiency limit')
hold on;grid on; xlim([-2 20]);ylim([0.1 10]);
yL = get(gca,'YLim');
line([-1.59 -1.59],yL,'Color','r','LineStyle','--');
The ultimate Shannon limit
From the plot in Fig. 1, we notice that the Shannon limit on $latex E_b/N_0$ is a monotonic function of $latex \eta_B$. When $latex \eta_B=2$, the Shannon limit on $latex E_b/N_0$ is equal to $latex 1.76 \; dB$. If $latex \eta_B=1$, the limit is at $latex 0\;dB$. When $latex \eta \rightarrow 0$, the Shannon limit on $latex E_b/N_0$ approaches $latex -1.59 \;dB$. This value is called ultimate Shannon limit or specifically absolute Shannon power efficiency limit. This limit informs us the minimum required energy per bit required at the transmitter for reliable communication. It is one among the important measures in designing a coding scheme.
The ultimate Shannon limit can be derived using L’Hospital’s rule as follows. The asymptotic value, $latex (E_b/N_0)_{min}$, that we are seeking, is the value of $latex E_b/N_0$ as the spectral efficiency $latex \eta$ approaches $latex 0$.
$latex \left(\frac{E_b}{N_0}\right)_{min}=\lim _{n \to 0}\left( \frac{E_b}{N_0} \right)=\lim_{n \to 0}\left( \frac{2^\eta -1 }{\eta}\right) \quad\quad (4) &s=2$
Let $latex f(\eta)=2^\eta-1$ and $latex g(\eta)= \eta$. As $latex f(0)=g(0)=0$ and the argument of the limit becomes indeterminate ($latex 0/0$), L’Hospital’s rule can be applied in this case. According to L’Hospital’s rule, if $latex \lim_{\eta \to k} f(\eta)$ and $latex \lim_{\eta \to k}g(\eta)$ are both zero or are both $latex \pm \infty$, then for any value of $latex k$.
$latex \lim_{\eta \to k} \left( \frac{f(\eta)}{g(\eta)} \right) = \lim_{\eta \to k} \left( \frac{f'(\eta)}{g'(\eta)} \right)\quad\quad (5) &s=2$
Thus, the next step boils down to finding the first derivative of $latex f(\eta)$ and $latex g(\eta)$. Expressing $latex 2^n$ in natural logarithm.
$latex 2 =e^{ln2} \quad\quad (6) &s=2$
$latex 2^\eta = (e^{ln2} )^{\eta}=(e^{\eta ln2}) \quad\quad (7) &s=2$
Let $latex u= \eta ln(2)$ and $latex y=e^u$, then by chain rule of differentiation,
$latex f'(\eta) =\frac{d2^\eta}{d \eta} = \frac{dy}{d \eta} = \frac{dy}{du} \frac{du}{d \eta} = e^u ln(2) = e^{\eta ln 2} ln(2) \quad\quad (8) &s=2$
Since $latex g(\eta)=\eta$, the first derivative of $latex g(\eta)$ is
$latex g'(\eta) = 1 \quad \quad (9)&s=2$
Using equations (8) and (9), and applying L’Hospital’s rule, the Shannon’s limit on $latex E_b/N_0$ is given by

Unconstrained and constrained Shannon limit
The absolute Shannon power efficiency limit is the limit of a band-limited system irrespective of modulation or coding scheme. This is also called unconstrained Shannon power efficiency Limit. If we select a particular modulation scheme or an encoding scheme, we calculate the constrained Shannon limit for that scheme.
Shannon power efficiency limit does not depend on error probability. Shannon limit tells us the minimum possible $latex E_b/N_0$ required for achieving an arbitrarily small probability of error as $latex M \to \infty$, where $latex M$ is the number of signaling levels for the modulation technique, for BPSK $latex M=2$, QPSK $latex M=4$ and so on. It gives the minimum possible $latex E_b/N_0$ that satisfies the Shannon theorem. In other words, it gives the minimum possible $latex E_b/N_0$ required to achieve maximum transmission capacity ( $latex R=C$, where, $latex R$ is the rate of transmission and $latex C$ is the channel capacity). It will not specify error probability at that limit. Nor will it give any direction on coding technique that can be used to achieve that limit. As the capacity is approached, the system complexity will increase drastically. So the aim of any system design is to achieve that limit. For example, the error probability performances of Turbo codes are very close to Shannon limit [1].
As an example, let’s evaluate the performance of a 2-PAM (Pulse Amplitude Modulation) system and determine the maximum possible coding gain that can be achieved by the most advanced coding scheme. The methodology for simulating the performance of a 2-PAM system is described in chapter 5 and 6. Using this methodology, the performance of a 2-PAM system is simulated and plotted in Figure 2. The absolute Shannon power efficiency limits when the spectral efficiency is $latex \eta=0$ and $latex \eta=2$ are also referenced on the plot.
The spectral efficiency of an ideal 2-PAM system is $latex \eta=2 \;bits/second/Hz$. Hence, if the target bit error rate is $latex 10^{-5}$, then a coding gain of $latex 7.8\;dB$ can be achieved using powerful codes, if we have to maintain the nominal spectral efficiency at $latex \eta=2 \;bits/second/Hz$.
If there is no limit on the spectral efficiency, then we can let $latex \eta \rightarrow 0$. In this case, the absolute Shannon power efficiency limit is $latex -1.59 \;dB$ when $latex \eta \rightarrow 0$. Thus a coding gain of approximately $latex 11 \; dB$ is possible with powerful codes if we let the spectral efficiency approach zero.
Rate this article: [ratings]
References
Related topics in this chapter
[table id=40 /]
Books by the author
[table id=23 /]