Solve Triangular Matrix – Forward & Backward Substitution

Key focus: Know the expressions to solve triangular matrix using forward and backward substituting techniques and the FLOPS required for solving it.

Forward Substitution:

Consider a set of equations in a matrix form , where A is a lower triangular matrix with non-zero diagonal elements. The equation is re-written in full matrix form as

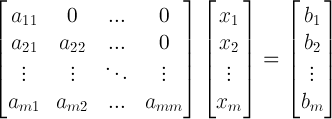
It can be solved using the following expressions

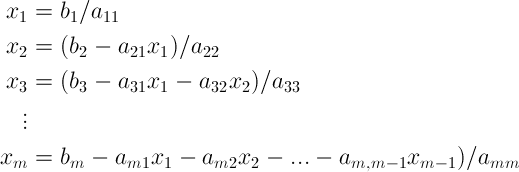
From the DSP implementation point of view, computation of requires one FLoating Point Operation per Second (FLOPS) – only one division. Computing will require 3 FLOPS – 1 multiplication, 1 division and 1 subtraction, will require 5 FLOPS – 2 multiplications, 1 division and two subtractions. Thus the computation of will require FLOPS.

Thus the overall FLOPS required for forward substitution is FLOPS

Backward substitution:

Consider a set of equations in a matrix form , where A is a upper triangular matrix with non-zero diagonal elements. The equation is re-written in full matrix form as

Solved using the following algorithm

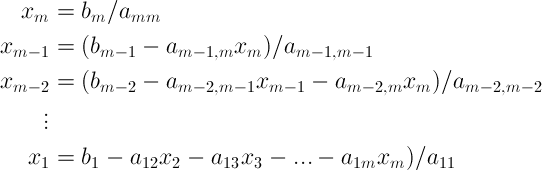
This one also requires FLOPS.

Rate this article: (51 votes, average: 3.61 out of 5)

More on Estimation Theory:

[1]	An Introduction to Estimation Theory
[2]	Bias of an Estimator
[3]	Minimum Variance Unbiased Estimators (MVUE)
[4]	Maximum Likelihood Estimation
[5]	Maximum Likelihood Decoding
[6]	Probability and Random Process
[7]	Likelihood Function and Maximum Likelihood Estimation (MLE)
[8]	Score, Fisher Information and Estimator Sensitivity
[9]	Introduction to Cramer Rao Lower Bound (CRLB)
[10]	Cramer Rao Lower Bound for Scalar Parameter Estimation
[11]	Applying Cramer Rao Lower Bound (CRLB) to find a Minimum Variance Unbiased Estimator (MVUE)
[12]	Efficient Estimators and CRLB
[13]	Cramer Rao Lower Bound for Phase Estimation
[14]	Normalized CRLB - an alternate form of CRLB and its relation to estimator sensitivity
[15]	Cramer Rao Lower Bound (CRLB) for Vector Parameter Estimation
[16]	The Mean Square Error – Why do we use it for estimation problems
[17]	How to estimate unknown parameters using Ordinary Least Squares (OLS)
[18]	Essential Preliminary Matrix Algebra for Signal Processing
[19]	Why Cholesky Decomposition ? A sample case:
[20]	Tests for Positive Definiteness of a Matrix
[21]	Solving a Triangular Matrix using Forward & Backward Substitution
[22]	Cholesky Factorization - Matlab and Python
[23]	LTI system models for random signals – AR, MA and ARMA models
[24]	Comparing AR and ARMA model - minimization of squared error
[25]	Yule Walker Estimation
[26]	AutoCorrelation (Correlogram) and persistence – Time series analysis
[27]	Linear Models - Least Squares Estimator (LSE)
[28]	Best Linear Unbiased Estimator (BLUE)

Books by the author

Wireless Communication Systems in Matlab Second Edition(PDF) (182 votes, average: 3.64 out of 5) $14.99 – Add to Cart Checkout Added to cart	Digital Modulations using Python (PDF ebook) (137 votes, average: 3.57 out of 5) $14.99 – Add to Cart Checkout Added to cart	Digital Modulations using Matlab (PDF ebook) (137 votes, average: 3.64 out of 5) $14.99 – Add to Cart Checkout Added to cart
Hand-picked Best books on Communication Engineering Best books on Signal Processing